某日，一学生到图书馆借了 N 本书，出图书馆的时候，警报响了，于是保安把该学生拦下，要检查一下哪本书（假设只有一本）没有登记出借。有什么方法？

我们把这个场景用数学模型表示出来：

Q：给定一个整型有序数组，如何找出某一整数是否在该数组中，以及该整数对应的下标？

什么意思呢？给定一个有序数组，有以下两种情况：

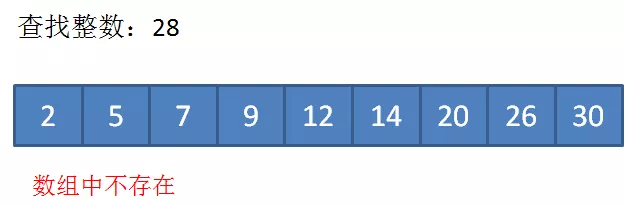
比如在该数组中查找整数 9，存在，所以返回 Index 为 3，如果要查找 28，数组中没有这个数，则返回数据不存在。

Traversal

最常用的方法，逐个遍历数组中的元素，将其和要查找的整数作比较，如果发现某个元素和要查找的整数相等，就返回它的下标。

回到文章开头的场景，就是把每一本书在防盗警报器中过一遍，以找到引发警报的书。

这种方法由于要遍历整个数组，时间复杂度为 O(N)。

Hash Table

为了节省时间，我们可以考虑建立一个哈希表，用数组元素作为 key，下标作为 value，后面查找任何整数的时候，直接查哈希表就行了。

如果要回到文章开头的场景，这种方法比较难比喻，可以理解为，借书的时候，图书馆为每一本要出借的书都贴一张标签，表明这本书是出借的，查找的时候只要看哪本书没有贴这个出借的标签即可。

这种方法时间复杂度为 O(1)，但是空间复杂度为 O(N)。

Binary Search

有没有一种方法，既可以让时间复杂度低于 O(N)，又不占用额外存储空间呢？

就是本文要介绍的二分查找了，通常也叫做折半搜索或对数搜索，是一种在有序数组中查找某一特定元素的搜索算法。

其实该方法在我们生活中也十分常用，比如我们玩一个猜数字的游戏，被猜方在心里想一个 1000 以内的自然数，猜测方猜的数字比被猜方的数字大，被猜方就说“大了”，猜测方猜的数字比被猜方的数字小，被猜方就说“小了”，一直到猜测为止。

最理想的方法如下：

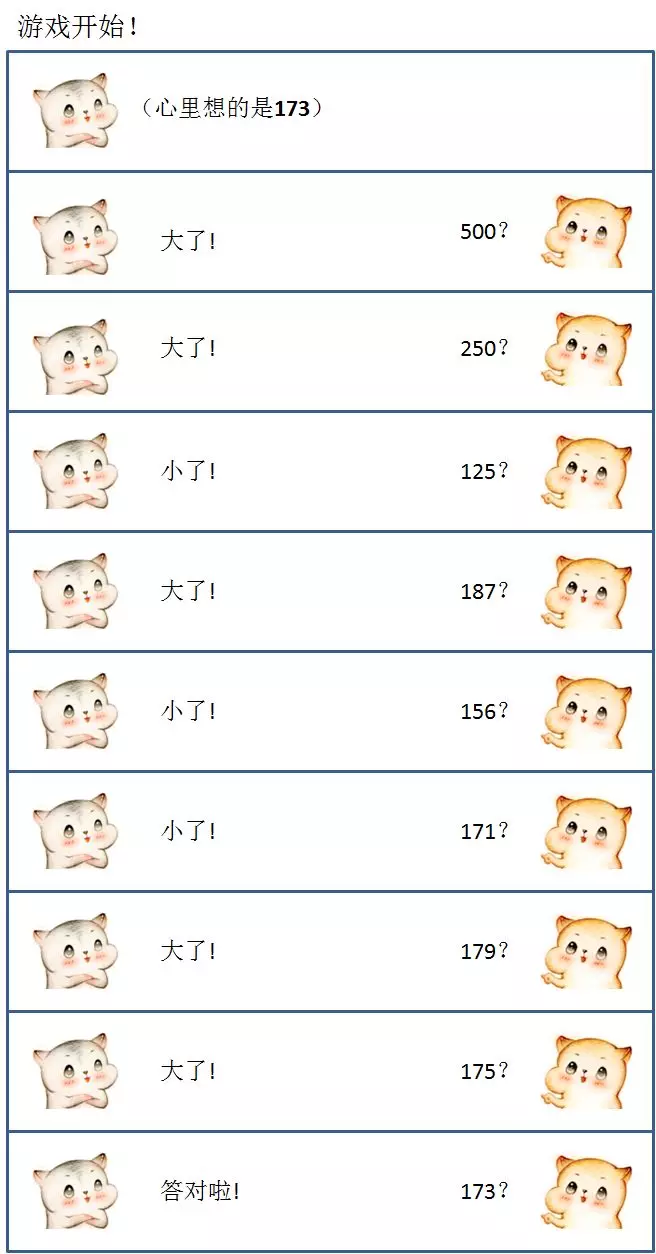
以上的仅需要 9 次就猜出了 1000 以内的数字，这里用到的就是二分查找的思想，每一次猜测，都选取一段整数范围的中位数，是效率最高的策略。

为什么说这样效率最高呢？因为每一次选择数字，无论偏大还是偏小，都可以让剩下的选择范围缩小一半。

给定范围 0 到 1000 的整数：

第一次我们选择 500，发现偏大了，那么下一次的选择范围，就变成了 1 到 499：

第二次我们选择 250，发现还是偏大了，那么下一次的选择范围，就变成了 1 到 249：

第三次我们选择 125，发现偏小了，那么下一次的选择范围，就变成了 126 到 249：

以此类推，最坏的情况需要猜测多少次呢？答案是 log₂1000=10 次，也就是让原本的区间范围进行 10 次 “折半”。

再来看看封面图的 Mario 找蘑菇，也是使用了折半查找的方法：

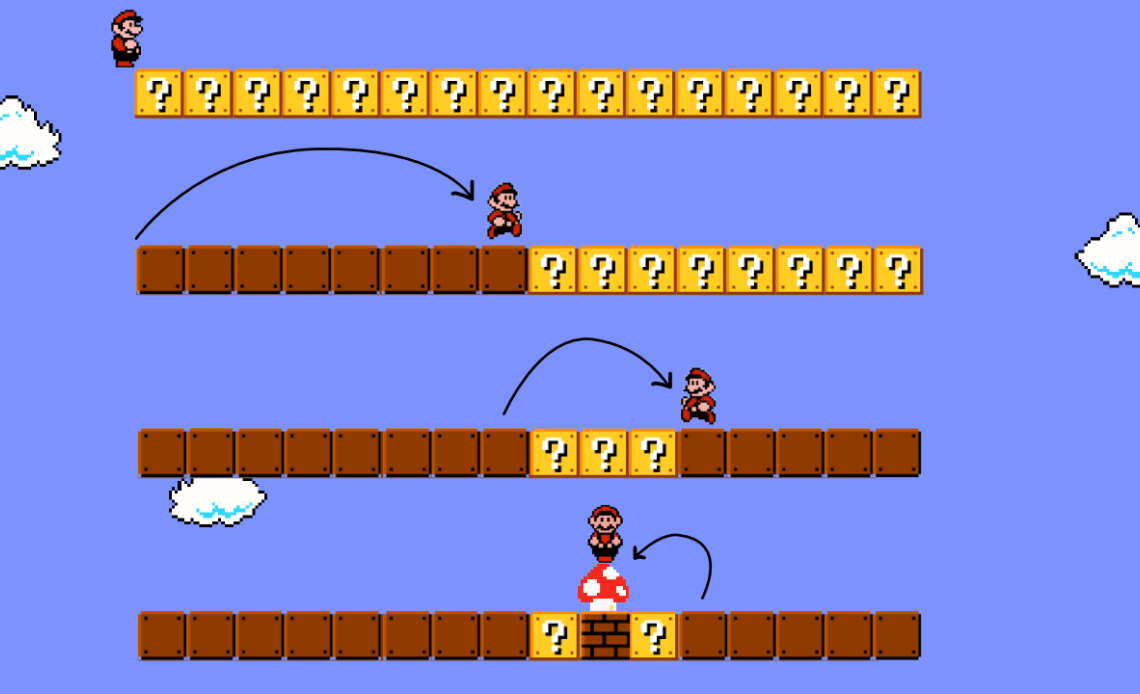
回到文章开头的场景，就是把书分成两堆，把第一堆在防盗警报器中过一遍，警报响了，再把这堆书分成两堆，如此反复，直到找出这本书为止。

这种方法的时间复杂度为 O(logN)。

接下来看看代码实现。

递归实现如下：

/**
 * 二分查找 - 递归
 *
 * @param arr  有序数组
 * @param key  需要查找的数
 * @param low  低位
 * @param high 高位
 * @return key 对应的位置
 */
public static int binarySearch(int[] arr, int key, int low, int high) {
    if (arr == null || low > high || key < arr[low] || key > arr[high]) {
        return -1;
    }
//  int mid = low + (high - low);
    int mid = (low & high) + ((low ^ high) >> 1);
    if (key > arr[mid]) {
        return binarySearch(arr, key, mid + 1, high);
    } else if (key < arr[mid]) {
        return binarySearch(arr, key, low, mid - 1);
    } else {
        return mid;
    }
}

非递归实现如下：

/**
 * 二分查找 - 非递归
 *
 * @param arr 有序数组
 * @param key 需要查找的数
 * @return key 对应的位置
 */
public static int binarySearch(int[] arr, int key) {
    int low = 0;
    int high = arr.length - 1;
    int mid;
    if (arr == null || arr.length <= 0 || key < arr[low] || key > arr[high]) {
        return -1;
    }
    while (low <= high) {
//      mid = low + (high - low);
        mid = (low & high) + ((low ^ high) >> 1);
        if (key > arr[mid]) {
            low = mid + 1;
        } else if (key < arr[mid]) {
            high = mid - 1;
        } else {
            return mid;
        }
    }
    return -1;
}

这里折半用到了『求两整数平均值』一文中提到的算法，以防止溢出，实际上在这里用减法代替加法（即代码中注释掉的部分）也是可以避免溢出，但官方的实现写法也是使用位运算。

我们可以再看看折半检索和线性检索在最优和最差情况下的区别的区别：

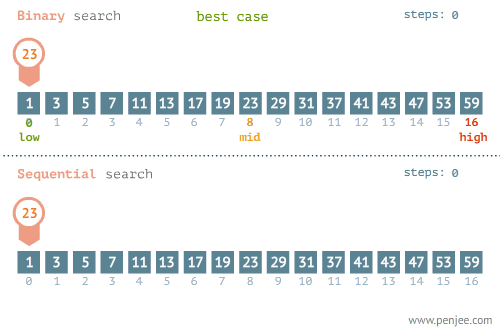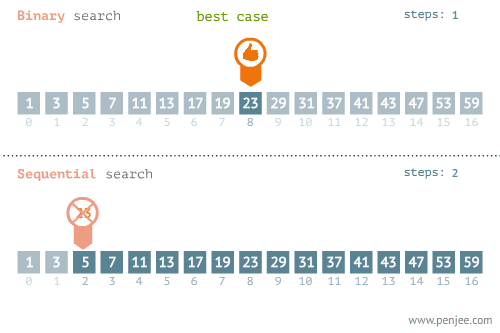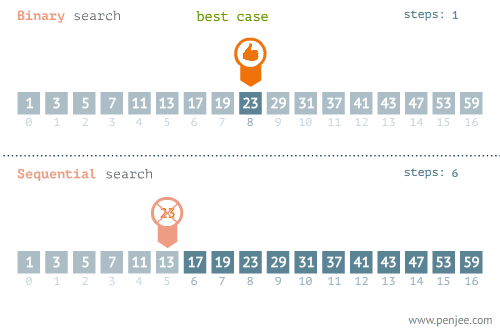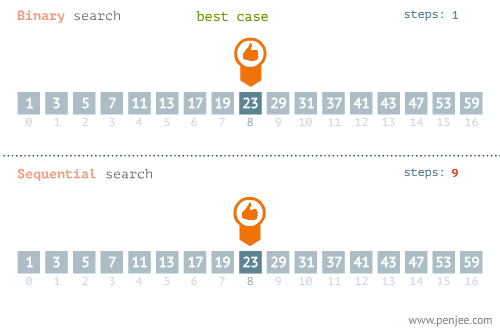
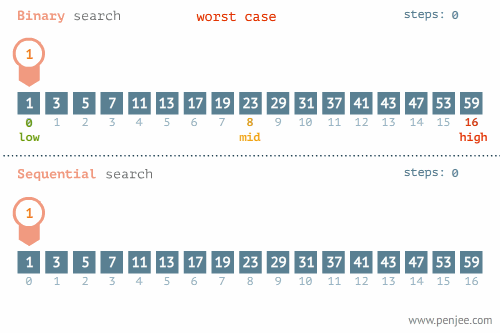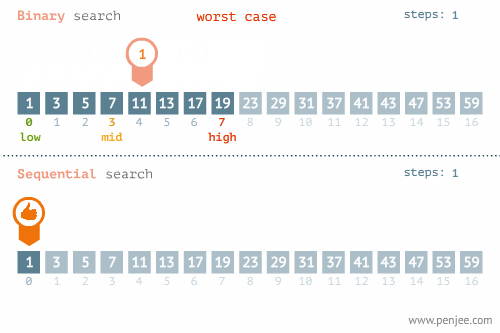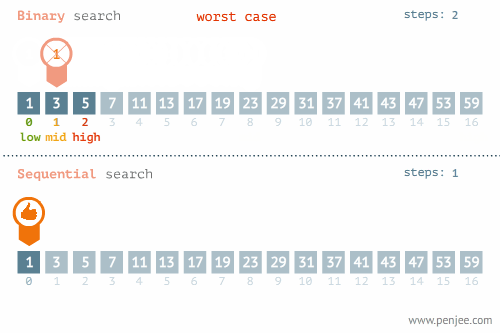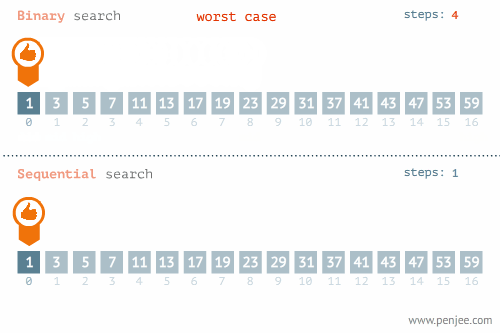
不要忘记了，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列，不满足这两个条件则无法使用。

顺便讲一个有趣的事，第一篇二分搜索论文是 1946 年发表的，然而第一个没有 Bug 的二分查找算法却是在 1962 年才出现，中间用了 16 年的时间。